Автор: uralpro.
В нескольких статьях мы рассмотрим использование индикатора PIN, который представляет собой вероятность присутствия на рынке так называемых информированных трейдеров. Статьи основаны на работе Paolo Zagaglia «PIN: Measuring Asymmetric Information in Financial Markets with R». Так как вероятность информированной торговли зависит от сделок купли и продажи в течение рабочего дня, в данном цикле мы рассмотрим весь процесс, от обработки исходных данных и вычисления вероятности информированной торговли, до определения параметров лежащей в основе математической модели. Примеры будут сопровождаться кодом на языке R.
Рост в последние годы алгоритмической и высокочастотной торговли открыл тот факт, что динамика биржевых цен сильно зависит от микроструктуры рынка. В частности, некоторые трейдеры могут иметь доступ к приватной информации о торгах, в то время как другие довольствуются только публичными новостями. Риск того, то неинформированный трейдер может в какой-то момент времени столкнуться в качестве контрагента в сделке с информированным, является одним из параметров, определяющих цену актива. Таким образом, измерение вероятности того, что контрагент владеет ассиметричной информацией, позволяет правильно вычислить цену.
Библиотека PIN языка R предоставляет инструменты для вычисления такой вероятности. Вычисление основано на расчете модели стратегического взаимодействия между трейдерами с разным информационным набором. В частности, вероятность информированной торговли зависит от числа сделок купли или продажи, происходящих на рынке.
Теоретическая модель.
Сделаем предположение. что рынок состоит из популяции трейдеров, одни из которых информированные, другие неинформированные. В течение дня маркет мейкер продает и покупает актив по ценам на биде и аске, которые он показывает публично. Так как стратегия маркет мейкера риск-нейтральная и он соревнуется с другими трейдерами в каждой транзакции, ожидаемая цена актива зависит от информации, которой владеет маркет мейкер в момент сделки.
Информационные события независимо распределены и появляются с вероятностью α. Хорошие новости возникают с вероятностью δ, плохие новости — с вероятностью 1−δ. В конце дня информационный набор каждого участника полный, и истинная цена актива реализована.
Маркет мейкер знает обе вероятности этих событий и порядок поступления информации на рынок. Тем не менее, он не знает, как событие повлияет на цену. Предположим, что маркет мейкер является байесовским в том смысле, что он использует информацию от поступившей сделки для коррекции своих представлений о произошедшем событии. Так как информация независима от одного дня к другому, структура модели позволяет изменять представления отдельно для каждого дня.
В представленной рабочей среде, рынок двигается теми трейдерами, которые получают сигналы об истинной цене актива, и получают преимущество от ассиметричной информации. Также присутствуют неинформированные трейдеры, которые не владеют такой информацией. Эти две группы участников входят в рынок с частотой, определенной независимым пуассоновским процессом каждую минуту в течение торгового дня.
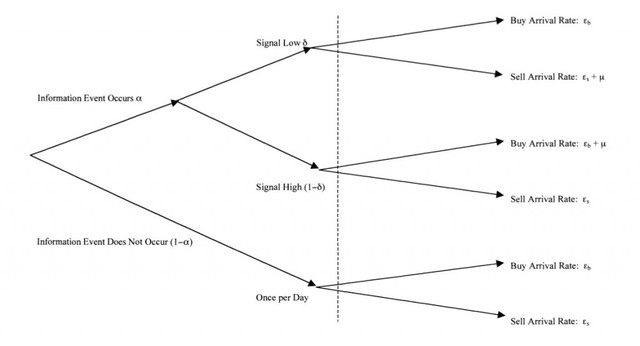
Информационное событие является причиной входа информированного трейдера в рынок. Например, если поступили «хорошие новости», такой трейдер покупает актив. Поступление новостей как на рынок,так и каждому трейдеру, следует независимому пуассоновскому процессу. Набор событий и соответствующих вероятностей изображен в виде дерева на рисунке в заглавии поста. В первом узле дерева определяется, поступила информация или нет. Если информация поступила, определяем «знак» новости. Три узла — «нет новостей», «хорошая новость», «плохая новость» , размещенные перед штриховой линией, появляются только раз в день. Для узла, выбранного в данный день, трейдеры поступают в соответствии с пуассоновским процессом. В день хороших новостей частота поступления ϵ+μ для ордеров на покупку и ϵ для ордеров на продажу. В день плохих новостей частота равна ϵ для ордеров на покупку и ϵ+μ для ордеров на продажу. В день отсутствия новостей только неинформированные трейдеры выставляют ордера с частотой ϵ.
Наблюдая изменения в стакане, трейдеры получают информацию о поступлении ордеров. Но они не знают мотивов сторон, участвующих в сделках. Другими словами, трейдеры не знают значения параметров для модели, описывающей наблюдаемые торговые паттерны. Тем не менее, эти параметры могут быть установлены из данных о поступлении ордеров.
В следующей статье рассмотрим эпирическую реализацию теоретической модели.
Другие алгоритмы, применяемые в алгоритмической торговле и биржевых роботах смотрите на моем сайте.