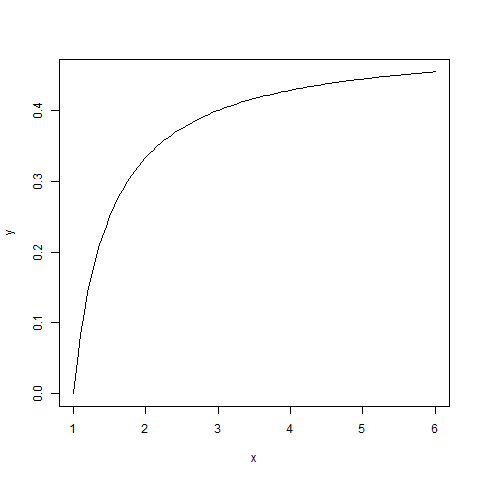Автор: Александр Кургузкин (mehanizator).
Ранее я предложил формулу для расчета правильной позиции по опциону, исходя из формулы для критерия Келли. Чтобы не было никаких сомнений, решил проверить формулу для покупки опциона численно.
Код на Java:
public static final int N = 10000;
public static final int NN = 100;
public static void main(String[] args) {
double p = 0.25;
double m = 1;
double k = (m — p) / (2 * m — p);
System.out.println(String.format(«p = %4.2f m = %5.3f k = %5.3f», p, m, k));
Random random = new Random();
for (double f = 0.025; f < 1; f += 0.025) {
double v = 0;
for (int i = 0; i < N; ++i) {
double equity = 1;
for (int j = 0; j < NN; ++j) {
double position = equity * f / p;
equity -= equity * f;
double res = random.nextDouble() > 0.5 ? 2 * m : 0;
equity += position * res;
}
v += Math.log(equity) / NN;
}
v /= N;
System.out.println(String.format(«f = %5.3f v = %+5.3f», f, v));
}
}
}
Здесь p — рыночная цена опциона, m — цена опциона по модели, k — оптимальный по Келли размер позиции, f — доля капитала под позицию, v — логарифм среднего изменения капитала на сделку. Моделируется игра, в которой с вероятностью в 0.5 опцион истекает в ноль, и с вероятностью 0.5 опцион дает прибыль 2*m.
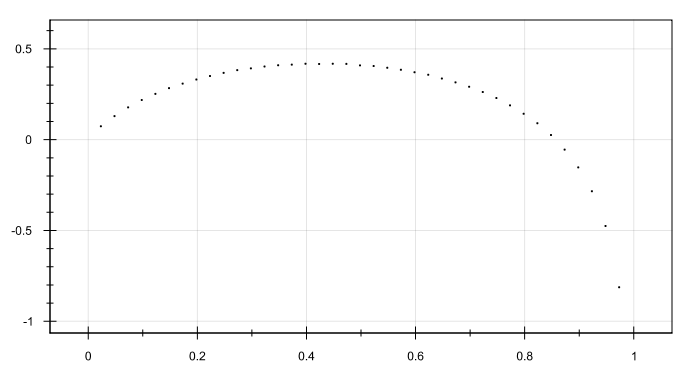
Для p = 0.25 и m = 1 (модельная оценка опциона в 4 раза выше рыночной цены) получаем по формуле k = 0.43, расчет:
f = 0.275 v = +0.377
f = 0.300 v = +0.387
f = 0.325 v = +0.397
f = 0.350 v = +0.404
f = 0.375 v = +0.407
f = 0.400 v = +0.413
f = 0.425 v = +0.411
f = 0.450 v = +0.413
f = 0.475 v = +0.411
f = 0.500 v = +0.403
f = 0.525 v = +0.400
f = 0.550 v = +0.390
f = 0.575 v = +0.379
…
Картинка:
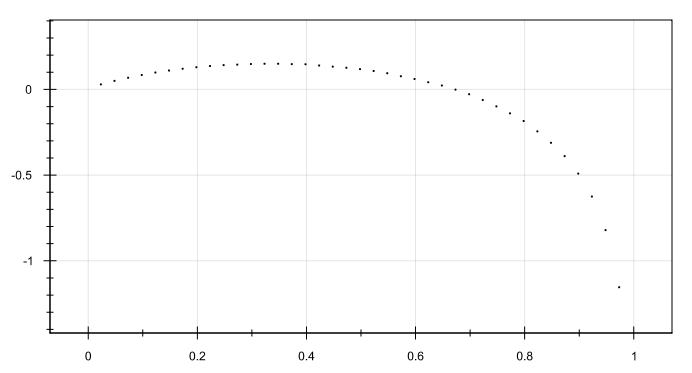
Для p = 0.5 и m = 1 (модель в два раза дороже рынка) k = 0.333, расчет:
f = 0.175 v = +0.115
f = 0.200 v = +0.124
f = 0.225 v = +0.131
f = 0.250 v = +0.136
f = 0.275 v = +0.139
f = 0.300 v = +0.142
f = 0.325 v = +0.144
f = 0.350 v = +0.144
f = 0.375 v = +0.142
f = 0.400 v = +0.141
f = 0.425 v = +0.134
f = 0.450 v = +0.127
f = 0.475 v = +0.121
f = 0.500 v = +0.113
…
Картинка:
Как видно, расчет подтверждает формулу.
Если ввести переменную y = m/p, то есть коэффициент превышения модельной ценой рыночной цены, то формулу для оптимального размера позиции по Келли можно переписать так:
k = (y — 1)/(2*y — 1)
График этой функции выглядит так:
Настоятельно рекомендуется использовать не полный размер позиции по Келли, а умножать его на 0.1-0.5 в зависимости от вашей склонности к риску. Выше полу-Келли нет смысла наращивать размер позиции, поскольку резко возрастающие риски задавят потенциальный дополнительный рост. Лично я обычно использую 0.1-0.25 Келли.
Автор: mehanizator
Комментарии:
serg: цитата : «Настоятельно рекомендуется использовать не полный размер позиции по Келли, а умножать его на 0.3-0.5 в зависимости от вашей склонности к риску.»
или 1*0,3=0,7 позици от Келли ?
Или 1*1,3=1,3 позиции от Келли ?
как правильно ?
Спасибо…
mehanizator: 1*0.3 = 0.3, каким образом у вас получилось 0.7?
serg: конечно 0,3…))
mehanizator: 0.3 позиции от Келли правильно.
serg: спасибо…
Vitas: келли вообще ошибочен, если уж на то пошло 😉
я численными методами нахожу оптимальный f, причем на выборке, по которой произвожу поиск искусственно увеличиваю кол-во плохих рез-ов — эмпирика конечно, но все же лучше чем использовать формулу в ситуации, к которой она не предназначена 😉