Распределение с «толстыми хвостами» (fat-tailed distribution) — это распределение вероятности, которое, наряду с другими распределениями с «тяжелыми хвостами» (heavy-tailed distributions), имеет особенность проявлять большой коэффициент асимметрии (skewness) или эксцесс (kurtosis). Сравнение «толщины» часто делается относительно нормального распределения или экспоненциального распределения. Распределения с «толстыми хвостами» на практике встречались в различных областях: экономике, физике и геологии. Некоторые распределения с «толстыми хвостами» обладают в хвостах убыванием по экспоненциальному закону, но совсем не обязательно, что они ведут себя так на всей протяженности.

Определение
Говорят, что распределение случайной величины X имеет «толстый хвост», если

То есть, если X имеет функцию плотности вероятности  ,
,
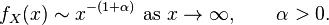
Здесь знак «~» относится к асимптотической эквивалентности функций. Некоторые называют распределением с «толстым хвостом» такое распределение, где 0 < α < 2 (т.е. только в случаях с бесконечной дисперсией).
Толстые хвосты и искажения оценки риска

Различные распределения Коши для различного параметров расположения и масштаба. Распределения Коши являются примерами распределений с «толстыми хвостами».
В отличие от распределения с «толстыми хвостами», в нормальном распределении события, которые отклоняются от среднего значения на пять и более стандартных отклонений («5-сигма») встречаются крайне редко, а с 10 или более сигма практически невозможны. С другой стороны, распределения с «толстыми хвостами», такие как распределение Коши (и все другие устойчивые распределения, за исключением нормального распределения) являются примерами распределений с «толстыми хвостами», которые имеют «бесконечную сигму» (технически говоря, дисперсия отсутствует).
Таким образом, когда данные естественным образом возникают из распределения с «толстыми хвостами», использование нормальной модели распределения рисков – и оценки соответствующей сигмы, неизбежно основанной на размере выборки конечного объема – очень снизит истинную степень сложности прогнозирования. Многие – в частности Бенуа Мандельброт (Benoît Mandelbrot), а также Нассим Талеб (Nassim Taleb) – отметили этот недостаток нормальной модели распределения и предположили, что распределения с «толстыми хвостами», такое как устойчивое распределение, описывающее доходности активов, часто встречаются в области финансов.
Модель ценообразования опционов Блэка-Шоулза основана на нормальном распределении. Если распределение на самом деле является распределением с «толстыми хвостами», то модель будет недооценивать опционы, которые далеко «вне денег», поскольку события 5 или 7-сигма гораздо более вероятны, чем спрогнозировало бы нормальное распределение.
Проявления в экономике
В области финансов толстые хвосты считаются неприятным явлением из-за дополнительного подразумеваемого ими риска. Предположим, у нас есть инвестиционная стратегия с годовой ожидаемой доходностью в пять раз больше стандартного отклонения. При нормальном распределении вероятность неудачи (получения отрицательной доходности) меньше, чем один на миллион, но на практике это число может быть больше. Нормальные распределения возникают в области финансов обычно потому, что факторы, влияющие на стоимость актива или цену, математически стабильны, и Центральная предельная теорема обеспечивает такое распределение. Однако, негативные события реального мира (например, нефтяной шок, крупное банкротство корпорации или резкое изменение политической ситуации), как правило, математически не стабильны.
Исторические примеры включают Черный понедельник (1987), пузырь дот-комов, финансовый кризис конца 2000-х годов, и отмену поддержки курса некоторых валют.
Толстые хвосты в распределениях рыночной доходности также имеют некоторое поведенческое происхождение (чрезмерный оптимизм или пессимизм инвесторов приводит к большому движению рынка), и поэтому изучаются в поведенческих финансах.
В маркетинге часто встречается известное правило «80-20» (например, «на 20% клиентов приходится 80% прибыли»), которое является проявлением распределения с «толстыми хвостами», лежащего в основе данных.
«Толстые хвосты» также наблюдаются на товарных рынках или в звукозаписывающей индустрии. Функция плотности вероятности для логарифма еженедельных продаж записей изменяется с сильным положительным эксцессом и характеризуется более узким и высоким максимумом и более толстым хвостом, чем в случае гауссовского распределения. С другой стороны, это распределение имеет только один толстый хвост, связанный с увеличением продаж за счет продвижения новых записей, которые становятся хитами.
Проявления в геополитике
В своей книге «Толстый хвост: сила политического знания для стратегического инвестирования» (The Fat Tail: The Power of Political Knowledge for Strategic Investing), политологи Ян Бреммер (Ian Bremmer) и Престон Кит (Preston Keat) предлагают использовать концепцию толстых хвостов к геополитике. Как заметил Уильям Safire (William Safire) в своем определении термина, толстые хвосты образуются, когда существует неожиданно толстый конец или «хвост» на конце функции плотности распределения, что указывает на аномально высокую вероятность катастрофичных событий. Это означает риск возникновения такого события, которое произойдет с низкой вероятностью, и которое трудно спрогнозировать, так что многие предпочитают просто его игнорировать. Один пример, который Бреммер и Кит выделили в книге – девальвация и дефолт России в августе 1998 года. Накануне этого события экономические аналитики прогнозировали, что в России не будет дефолта, потому что у страны была возможность и готовность продолжать осуществлять взаиморасчеты. Однако политологи утверждают, что разобщенное политическое руководство России и отсутствие регулирования рынка – наряду с фактом, что некоторые влиятельные чиновники России выиграли бы от дефолта – уменьшило готовность России платить. Поскольку эти политические факторы отсутствовали в экономических моделях, экономисты не смогли верно оценить вероятность дефолта.
Источник: Wikipedia.org: Fat-tailed distribution
Другие статьи по теме:
Как защитить инвестиционный портфель от краха: паритет хвостового риска
Общие статистические свойства ценовых движений (Stylized facts)
Хвостовой риск «малорискованных» активов недооценивается