В финансах волатильностью называют меру изменчивости цены финансового инструмента во времени. Историческая волатильность выводится из временной серии прошлых рыночных цен. Вмененная волатильность выводится из рыночных цен торгуемых деривативов (в частности опционов). Для волатильности используется символ σ, который соответствует стандартному отклонению.
На современных рынках есть возможность торговать волатильностью непосредственно, через использование производных инструментов, таких как опционы и свопы (Арбитраж волатильности).
Обычно под волатильностью имеют в виду текущую волатильность финансового инструмента за определенный период (например 30 дней или 90 дней). Эта волатильность основана на исторических ценах за период, куда входит самая последняя цена. Кроме текущей волатильности, используются еще следующие термины:
— Историческая волатильность: волатильность финансового инструмента за определенный период, но с последним наблюдением на некоторый момент прошлого.
— Будущая волатильность, которая относится к волатильности за определенный период, начинающийся в текущий момент и заканчивающийся в будущем (обычно в момент экспирации опциона).
— Текущая вмененная волатильность, которая выводится из текущих цен опционов.
— Историческая вмененная волатильность, которая относится к вмененной волатильности на какой-то момент в прошлом.
— Будущая вмененная волатильность, относящаяся ко вмененной волатильности на определенный момент в будущем.
Волатильность не определяет направление ценовых изменений, а только их разброс. Это происходит потому, что при вычислении стандартного отклонения все изменения цены возводятся в квадрат, таким образом и положительные и отрицательные изменения цены комбинируются в одно значение. Два инструмента с разными волатильностями могут иметь одинаковое мат.ожидание, но инструмент с большей волатильностью будет иметь большие колебания в стоимости за рассматриваемый период времени. Например, акция с низкой волатильностью может иметь ожидаемый (средний) результат в 7% с годовой волатильностью 5%. Это говорит о возможном результате с примерно -3% до +17% с вероятностью 95% (две сигмы). Акция с большей волатильностью 20% и тем же ожиданием в 7% даст диапазон от -33% до +47% с вероятностью 95%. Эти оценки предполагают нормальное распределение ценовых изменений, хотя реальные распределения имеют эксцесс.
Для финансовых инструментов, изменения цен которых подчиняются законам случайного гауссовского блуждания или виннеровского процесса, ширина распределения возрастает по мере увеличения времени. Это потому, что существует возрастающая вероятность того, что цена инструмента уйдет дальше от начальной точки с течением времени. Однако, увеличение волатильности происходит не линейно, а по закону квадратного корня от времени, поскольку некоторые изменения цены гасят друг друга, значит отклонение за удвоенное время не будет вдвое большим.
Поскольку изменения цены не следуют гауссовскому распределению, часто используются другие распределения, такие как распределение Леви. Это помогает описать особенности, такие как “тяжелые хвосты”.
Расчет волатильности
Годовая волатильность σ расчитывается как стандартное отклонение годовых логарифмических ценовых изменений.
Волатильность для произвольного периода времени Т выражается через годовую следующим образом:

Следовательно, если дневные логарифмические изменения цен имеют стандартное отклонение σ(SD), годовая волатильность считается так:
![]()
Обычно считается, что P = 1/252 (где 252 — число торговых дней в году). Если σ(SD) = 0.01, годовая волатильность:

Месячная волатильность (T = 1/12) будет:

Эти формулы предполагают, что процесс изменения цен описывается случайным блужданием или виннеровским процессом, чьи изменения имеют конечную дисперсию. Однако, в общем случае, для естественных стохастических процессов, точное взаимоотношение волатильностей на разных временных горизонтах более сложное. Некоторые используют экспоненту Леви для экстраполяции естественного процесса:
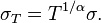
Если α = 2, получаем отношение для виннеровского процесса, но многие считают, что α < 2 для финансовых инструментов. Бенуа Мандельброт исследовал цены на хлопок и обнаружил, что для них α = 1.7.
Несмотря на множество сложных моделей предсказания волатильности, критики заявляют, что их предсказательная способность такая же, как и у более простых методов, как например брать просто прошлую волатильность. Некоторые, впрочем, утверждают, что критикам просто не удалось заставить работать эти сложные модели.
Источник: en.wikipedia.org
Другие статьи по теме:
Вмененная волатильность (implied volatility)