Автор: Александр Кургузкин (mehanizator).
Если посмотреть на динамику моментов распределения по годам, можно заметить, что в периоды низкой волатильности ассимметрия и эксцесс близки к нулю, а заметными они становятся в годы рыночной турбулентности. Было бы интересно взглянуть на зависимость моментов распределения от волатильности.
Для каждой даты в прошлом у нас есть значение прошлой волатильности за 21 торговый день (календарный месяц) и значение логарифма будущего изменения на месяц вперед, нормированное на прошлую волатильность. Ранжируем массив по значению прошлой волатильности, дальше проходимся по полученному массиву окном в 252 бара и считаем моменты распределения внутри этого окна.
Данные по индексу S&P 500 берем с 1994 года, получается 4870 значений. По горизонтальной оси — логарифм прошлой волатильности. Вот что получается:
Среднее:
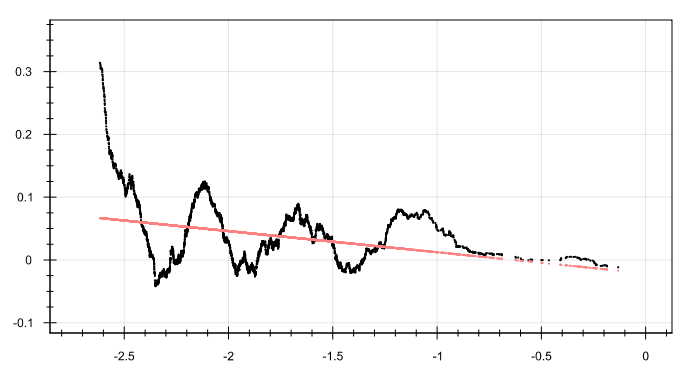
Стандартное отклонение:
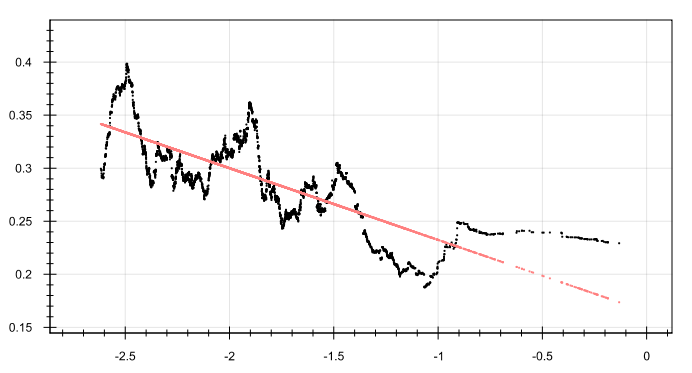
Ассимметрия:
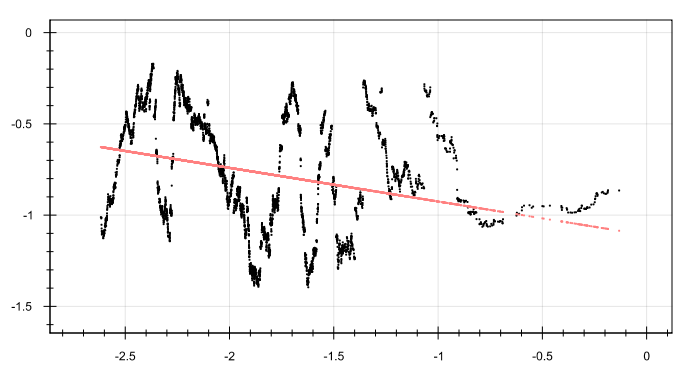
Эксцесс:
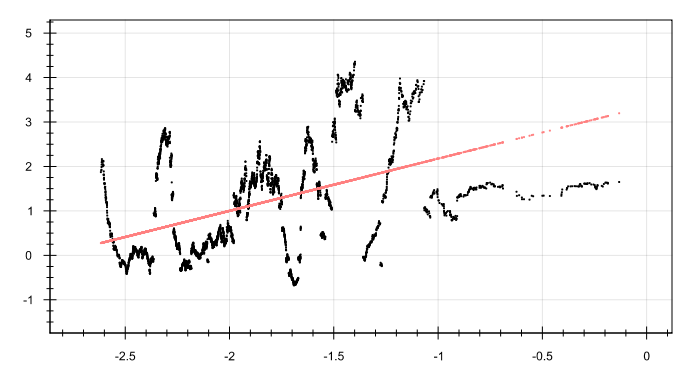
Красными линиями приведены модели регрессии:
mean = -0.0228 — 0.0337 * x, r: -0.2886
sigm = +0.1642 — 0.0676 * x, r: -0.7489
skew = -1.1147 — 0.1846 * x, r: -0.2652
kurt = +3.3238 + 1.1755 * x, r: +0.4602
где x — логарифм прошлой волатильности.
Интерпретируем полученные картинки
Зависимость матожидания от волатильности это известный stylized fact, который называется «эффект плеча» — цены склонны расти при невысокой волатильности и падать при высокой.
Зависимость стандартного отклонения будущих изменений (то есть фактически будущей волатильности) от прошлой — отражение цикличности волатильности, ее тенденции возвращаться к среднему. Низкая волатильность влечет расширение волатильности, высокая — сокращение волатильности.
Ну, и зависимость ассимметрии и эксцесса от волатильности наверное комментариев не требует. Чем выше волатильность, тем более распределение кривое и хвостатое.
Итак, у нас есть модели для моментов распределений, теперь можно по этим моментам восстанавливать распределение, например Johnson SU/SB, и считать цены опционов.
Автор: mehanizator