Инвесторы обычно используют коэффициент Шарпа или коэффициент Сортино для того, чтобы ранжировать и сравнивать взаимные фонды, ETF или индексные инструменты. Однако, эти распространенные бенчмарки доходности имеют несколько недостатков, которые могут часто сбивать с толку. Коэффициент Омега лишен этих недостатков и дает более глубокий метод ранжирования инвестиционных инструментов.
Коэффициент Шарпа был предложен в 1960-х годах, также он известен как коэффициент прибыль/риск. Он представляет собой эффективную доходность фонда поделенную на его стандартное отклонение и его главное преимущество в том, что он широко представлен у разных поставщиков данных. Стандартное отклонение применяется в коэффициенте Шарпа как приближение к риску. Однако, такой подход может сбивать с толку по нескольким важным причинам.
Во-первых, стандартное отклонение предполагает, что результаты инвестирования распределены по нормальному закону. Другими словами, изменения должны иметь классическую колоколообразную форму. Для многих инвестиционных инструментов это может быть не так. Хедж фонды и другие инвестиционные стратегии могут показывать асимметрию и эксцесс в результатах.
Во-вторых, большинство инвесторов думают о риске как о вероятности получить убыток, то есть риск это размер левой части распределения. Стандартное отклонение же показывает как широко распределены изменения вокруг среднего. Игнорируя информацию о распределении изменений, стандартное отклонение может не вполне адекватно представлять риск экстремальных потерь.
В-третьих, стандартное отклонение в равной степени наказывает разброс изменений выше среднего и ниже среднего. Однако большинство инвесторов беспокоятся только о измерениях ниже среднего, и одобряют изменения выше среднего. Этот момент был учтен в коэффициенте Сортино, который аналогичен коэффициенту Шарпа, но наказывает только отрицательные отклонения.
Наконец, для представления ожидаемой доходности используются средние исторические величины. Это опять же может вводить в заблуждение, поскольку усреднение дает равные веса данным из далекого прошлого и из недавнего прошлого. Последние должны быть более адекватной оценкой будущих результатов, чем первые.
Коэффициент Омега был разработан чтобы исправить недостатки коэффициента Шарпа. Коэффициент Омега определяется как площадь области функции распределения, расположенной выше цели, деленная на площадь области ниже цени. Другими словами, это взвешенные по вероятности прибыли поделенные на взвешенные по вероятности убытки. Этот подход изящно включает всю критическую информацию по распределению изменений, и что более важно адекватно отражает риск экстремальных потерь.
Однако, инвестиционные инструменты с высоким коэффициентом Омега могут быть более волатильными, чем таковые с высоким коэффициентом Шарпа.
Коэффициент Омега определяется следующей формулой:
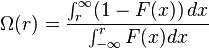
F(x) здесь кумулятивная функция распределения, т.е.вероятность того, что изменение будет меньше x.
r это цель (бенчмарк), выбранная инвестором.
Коэффициент Омега легко можно рассчитать с помощью Excel. Если ячейки A1:A15 содержат результаты инвестиционного инструмента, а B1 содержит цель (бенчмарк), коэффициент Омега определяется формулой:
Автор: Samir Khan
Источник: The Omega Ratio — A Better Investment Performance Benchmark
Комментарии:
Andrew Kartashov: Ага, вчера нашел и ее тоже =) Формула красивая и сказан красиво
«Наконец, для представления ожидаемой доходности используются средние исторические величины. Это опять же может вводить в заблуждение, поскольку усреднение дает равные веса данным из далекого прошлого и из недавнего прошлого. Последние должны быть более адекватной оценкой будущих результатов, чем первые»
Однако упрощенная версия в екселе ничего этого не учитывает. Тупо делит среднее одно на другое с одинаковыми весами.
mehanizator: да, подозрительно.
MrJOKER: какую r было бы логично брать?
MrJOKER: «Омега показывает на сколько будет удовлетворена эта минимальная доходность.» т.е. r.
mehanizator: r это доходность вашего бенчмарка, по которому вы меряетесь. универсального ответа тут нет. но я обычно при расчетах коэффициентов подобного рода беру ноль 🙂
Vitas: этот коэффициент по сути дела почти не наказывает за редкие но очень большие убытки. на самом деле надо стремится к контролированию рисков и подрезанию убытков, именно это дает возможность хорошо и стабильно (насколько вообще слово стабильно применимо к торговле) зарабатывать на рынке. Я пробовал самые разные метрики, некоторые из них неплохие. но что самое смешное, банальное среднее ГЕОМЕТРИЧЕСКОЕ всех сделок оказалось очень неплохим показателем.