При расчете симуляций по волатильности и квадратному корню из времени, я начал думать о том, какое время отслеживают опционы – календарное время, рыночное время или что-то среднее? При расчете VIX Чикагской опционной биржи (Chicago Board of Options Exchange, CBOE) используется календарное время, 365 дней в году, но большинство опционных гуру для расчета волатильности рекомендует использовать 252 дня – стандартное число торговых дней в году на рынках США.
Когда дело доходит до распада опционов, большинство людей, в том числе и гуру, считают, что стоимость опционов уменьшается, когда рынки закрыты – точка зрения, которая, по-моему, конфликтует с подходом использования 252 дней при расчете волатильности на годовой основе.
Экспериментальное открытие, на котором основана современная теория распада опционов, произошло в 1825 году, когда ботаник Роберт Броун (Robert Brown) посмотрел через микроскоп на пыльцевые зерна, находящиеся в воде, и заметил, что они двигаются случайным образом. Он не смог объяснить это движение, но позже физики, в том числе и Альберт Эйнштейн, показали, что это был результат случайного столкновения молекул воды с пыльцой. Этот эффект был назван «Броуновское движение» в честь Броуна.
Если вы фактически остановите время в эксперименте Броуна (например, заморозите образец), пыльца перестанет двигаться. Или, если вы закроете казино на день (возможно, это лучший пример для рынка), собственные средства соответствующих игроков перестанут уменьшаться.
Сторонники подхода календарного времени отмечают, что существует большое число видов деятельности/событий с широкополосным воздействием, которые могут изменять стоимость базовых активов, пока рынок закрыт. Это, например, продление торговых часов, активность на зарубежных рынках, корпоративные заявления, геополитические события и стихийные бедствия.
Однако получается так, что большинство заслуживающих внимания событий, которые происходят за пределами рыночных часов, как правило, являются источниками плохих новостей. Например, в ближайшее время я не думаю, что увижу заголовки, заявляющие, что «ISIS расформировывается», «Мы поняли, что это было ужасным недоразумением» или «Безвредный оползень позволил обнаружить огромный тайник с золотом». Эта тенденция к отрицательным движениям за последние 20 лет отражена в средней годовой доходности для тех часов, когда рынок закрыт в -0,37% по сравнению с + 9,59% для рыночных часов. И плохие новости, как правило, заставляют цены опционов расти …
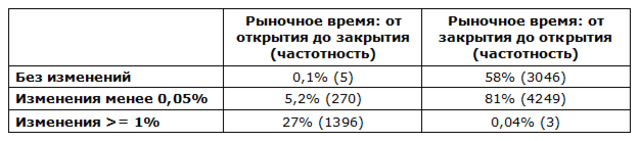
Если опционное время распространяется на период, когда рынки закрыты, я бы рассчитывал на то, что стоимость на момент открытия рынка будет отличаться от стоимости на момент закрытия. Ниже представлена выборка данных за последние 20 лет:
Я был удивлен тому, как часто рынок открывался без изменений после предыдущего закрытия (3046 раза) и как редко он изменялся за ночь гэпом более чем на + -1% (3 раза).
Так что же?
До сих пор мои аргументы отдавали преимущество рыночному времени по сравнению с календарным, но на самом деле так ли это? Практически существует два случая, где это имеет значение: динамика распада опционов и точность расчета вмененной волатильности близких к экспирации опционов.
Распад опционов
Начинающие опционные трейдеры, как правило, бывают разочарованы, когда пытаются получить прибыль от распада теты в выходные. Если базовый актив не изменяется, то цены опционов, как правило, в понедельник останутся без изменений с момента закрытия в пятницу. Специалисты объясняют это явление тем, что маркет-мейкеры не хотят оставаться с потерями теты на выходных и снижают цены, корректируя перед выходными свои модели.
Я думаю, что маркет-мейкеры правы, но по неверным причинам. Их компьютерные модели основаны (или, по крайней мере, были основаны) на календарном времени, что предполагает распад опционов в выходные дни. При корректировке своих моделей они определяют стоимость в зависимости от того, что действительно происходит – никакого распада, когда рынок закрыт.
Рассчитанные на годовой основе коэффициенты
Для долгосрочных прогнозов волатильности не имеет большого значения, какой подход вы используете. Для опционов, истекающих через месяц, разница во вмененной волатильности при использовании моделей с 365 и 252 днями составляет лишь несколько процентов. Однако для более коротких сроков экспирации разница может быть существенной.
На графике ниже представлено поминутное сравнение значений двух подходов и показана разница между ними в процентах. Подход с использованием календарного времени изображен черной линией, а рыночного времени – зеленой. Обратите внимание на то, как разница достигает максимума во время открытия в понедельник и уменьшается почти до нуля при закрытии в пятницу.
Рассчитанные на годовой основе коэффициенты рыночного и календарного времени
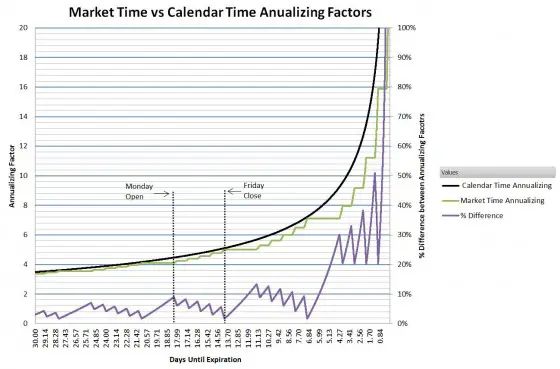
Ось Х – количество дней до экспирации
Черная линия – календарное время
Зеленая линия – рыночное время
Фиолетовая линия – разница в процентах
Этот эффект «выходных дней» иногда виден на индексе VIX СВОЕ, и он довольно сильно выражен со своим новым краткосрочным индексом VXST, что не удивительно, поскольку этот новый индекс основан на ценах опционов S&P 500 (SPX) с экспирацией не более 9 дней.
Есть веские причины для того, чтобы при расчете данных на год использовать календарные дни. В этом случае отсутствует чувствительность к праздникам, неожиданным остановкам рынка, а также к разнице в торговых календарях разных стран. Я думаю, что именно поэтому это стало фактическим стандартом в мире волатильности. Но рост краткосрочных продуктов волатильности, таких как недельные опционы, достаточно сильно изменил пейзаж волатильности, и я считаю, что мы должны, по крайней мере, знать, что является технически правильным.
Аналитический подход к решению
Обычно мы берем краткосрочную волатильность (например, дневную) и умножаем ее на соответствующий пересчитанный на год коэффициент, чтобы получить годовую волатильность. После того, как рассчитанные на годовой основе коэффициенты стали вызывать сомнение, я решил взять историческую годовую волатильность S&P 500 за последние 64 года и разделить ее на дневную волатильность, чтобы найти реальный исторический пересчитанный на год коэффициент.
Сначала я проверил правильность этого подхода методом Монте-Карло, который вычислил теоретический пересчитанный на год коэффициент для моделируемого 64-годового рыночного периода, а затем повторил это действие 10000 раз, чтобы получить статистику расчета. Затем я применил тот же расчет для доходности S&P 500 за последние 64 лет.
Для получения значения краткосрочной волатильности для каждого дня моделирования я использовал стандартное отклонение натурального логарифма дневных доходностей за предыдущие 252 дня. Для расчета годовой доходности я использовал смоделированную рыночную цену через год, разделенную на рыночную стоимость текущего дня. Отставание волатильности (volatility drag) является важным эффектом второго порядка, который должен быть учтен в расчетах. Я скорректировал фактические результаты с помощью среднего пересчитанного на год коэффициента роста, чтобы компенсировать ненулевое среднее значение фактической доходности за последние 64 года.
Результат представлен на следующем графике.
Моделирование рассчитанных на годовой основе коэффициентов волатильности (результаты приведены в квадрате)
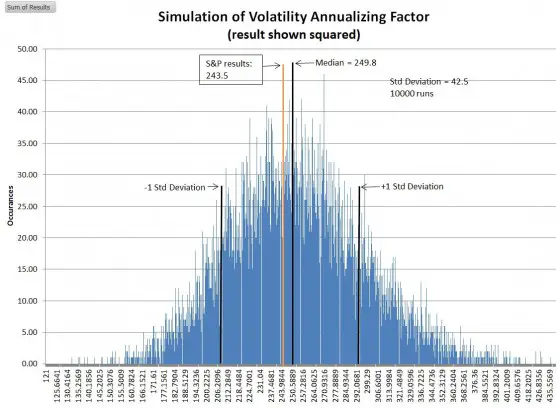
Квадрат пересчитанного на год коэффициента составляет лишь 0,87% от значения теоретической медианы, равной 252, а фактический результат S&P 500, равный 243,5, составляет лишь 2,5% от средней величины. Результат S&P, равный 243,5, соответствует почти 3-м сигмам от конкурирующей величины, равной 365.
Мои результаты моделирования имеют среднее значение 252,2 (погрешность равна 0,08%), если я использую коэффициент отставания волатильности 0,6 вместо стандартного 0,5. Я считаю, что моя модель чуть меньше корректирует отставание волатильности.
Данные S&P 500 согласуются с моделью, основанной на 252-х днях, которая не учитывает распад опционов, когда рынок закрыт. Данные также показывают, что когда вы видите подозрительно высокое значение краткосрочной волатильности в начале недели, то вы должны отнести это на счет несовершенных алгоритмов, а не на счет чего-то реального на рынке.
Автор: Vance Harwood
Источник: The Myth of Option Weekend Decay
Другие статьи по теме:
Искусство торговли волатильностью
Риск исполнения опционов, шортовые коллы и дивидендные даты
Перебалансировка портфеля с помощью опционов
Комментарии:
Vitas: продаем опционы по понедельникам? 😉