Выше изображены известные Треугольник Серпинского и Кривая Коха. Эти объекты являются «самоподобными», и это означает, что их исследование на более детальном уровне покажет ту же форму. Оба элемента являются примерами «фрактальной геометрии» и характерны для многих явлений в природе, таких как горы, кристаллы и газы. Самоподобные объекты ассоциируются с простотой, дублированием и, следовательно, надежностью. Объекты, которые не являются самоподобными, ассоциируются со сложностью и хаосом.
Некоторые математики (в том числе Бенуа Мандельброт (Benoit Mandelbrot)) заметили, что рынки явно являются негауссовыми, с не нормальным распределением. Рынки демонстрируют «толстые хвосты» и имеют распределение, которое имеет больше общего с распределением Леви, чем с нормальным распределением, часто используемым в количественных финансах. Но рынок не имеет постоянного распределения – порой поведение рынка носит довольно нормальный характер, а в других случаях рынок безумен и непредсказуем. Вопрос заключается в том, как мы можем эффективно определить, в каком режиме находится рынок, чтобы можно было применить соответствующие торговые стратегии для снижения рисков.
Суть самоподобия и сложности состоит в сравнении всех составных частей. Например, возьмем квадрат, который состоит из четырех отдельных квадратов одинакового размера. Площадь квадрата большей площади эквивалентна сумме площадей каждого из составных квадратов. Это, конечно, верно и для ограниченной линии, которая эквивалентна сумме частей.
Одним из методов выявления самоподобия на фондовом рынке является наблюдение за пределами изменения или разница между максимумами и минимумами. Мы ожидаем, что на совершенно самоподобном рынке больший диапазон будет эквивалентен сумме диапазонов, измеренных с меньшим интервалом. Чем более хаотичен рынок, тем больше будет разница между этими двумя мерами. Такие рыночные условия будут характеризоваться большим коэффициентом между суммой меньших диапазонов по сравнению с долгосрочным диапазоном. По существу эту взаимосвязь называют фрактальной размерностью, и она является мерой сложности.
Существует много разных способов ее измерения, включая использование показателя Хёрста, но проблема, с которой я всегда сталкивался во время собственного скромного исследования, заключается в том, что предлагаемые пороги, определяемые конкретными абсолютными значениями, кажется, не отражают информацию в соответствии с теорией. Я часто обнаруживал, что относительные меры, как правило, более надежны и корректны, аналогично тому, как размер прошлой доходности имеет меньшую прогностическую ценность, чем относительный ранг прошлой доходности. Относительные меры, как правило, более постоянны, чем абсолютные значения.
Чтобы вычислить меру самоподобия, я использую внутридневной диапазон (максимум минус минимум) по сравнению с более длительным окном. Вот как это рассчитывается:
1) находим максимум минус минимум для каждого из 10 дней, предшествующих настоящему моменту;
2) берем сумму этих значений (сумма частей);
3) находим 10-дневный диапазон: 10-дневный максимум минус 10-дневный минимум;
4) делим сумму частей на целый диапазон – это основная мера фрактальной размерности/сложности;
5) берем 60-дневную среднюю 10-дневной серии значений сложности – это метрика квартального хаоса/стабильности;
6) используем 252-дневное нормальное распределение z-оценки или ранг процентиля метрики хаоса/стабильности;
7) значения, которые выше 0,5, показывают, что рынок находится в режиме «хаоса» и гораздо менее предсказуем и нестационарен, значения ниже 0,5 показывают, что рынок стабилен и намного более предсказуем.
Когда рынок «стабилен», легче использовать эффективные количественные торговые системы. Когда рынок находится в режиме «хаоса» – при этом он не обязательно волатилен – то слишком сложно использовать стандартные измерения и определения характеристик основного линейного прогноза.
Давайте посмотрим, какие результаты показывает эта мера в течение длительного периода времени, используя S&P 500 в качестве тестового набора. Вот как вел себя рынок в обоих режимах в течение последних 50 с лишним лет:

Красная линия – на рынке хаос
Зеленая линия – рынок стабилен
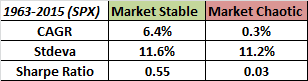
Рынок показывает очень плохие результаты в условиях «хаоса», и, кажется, получает всю долгосрочную доходность во время «стабильного» режима. Заметим, однако, что волатильность обоих режимов существенно не отличается – это означает, что мы ухватили нечто иное, чем просто уровень рыночной волатильности. Кроме того, корреляция между сигналами, указывающими на хаос, и, например, сигналом основного тренда 200-дневной скользящей средней составляет -0,116. Это означает, что мы также ухватили нечто иное, чем просто рыночный тренд. Индикатор предназначен для использования при определении режимов, а не в качестве торгового сигнала, чтобы идти в лонг или шорт, но определенно имеет некоторые интересные свойства, достойные дальнейшего изучения и уточнения.
Автор: David Varadi
Источник: Using a Self-Similarity Metric with Intraday Data to Define Market Regimes
Другие статьи по теме:
Общие статистические свойства ценовых движений (Stylized facts)
Пример подгонки распределения семейством Johnson
Фондовый рынок как искусственный хаос: почему погибают торговые системы
Комментарии:
EdgeStone: Статья интересная, но только не фига не понял, что за график он сделал?
На одной и той временной шкале отложены два графика поведения SnP в разных режимах одновременно, это вот как?
mehanizator: я так понимаю первая система в кеше когда вторая в позиции и соответственно наоборот.
EdgeStone: А, типа просто лонг, попеременно.
dobrachev: «5) берем 60-дневную среднюю 10-дневной серии значений сложности – это метрика квартального хаоса/стабильности;
6) используем 252-дневное нормальное распределение z-оценки или ранг процентиля метрики хаоса/стабильности;
7) значения, которые выше 0,5, показывают, что рынок находится в режиме «хаоса» и гораздо менее предсказуем и нестационарен, значения ниже 0,5 показывают, что рынок стабилен и намного более предсказуем. »
Я не понимаю, итоговое значение (которое с 0,5 сравнивают) оно откуда берётся? Как его надо рассчитывать? Это 60-дневная средняя 10-дневной серии значений сложности? Или мы результат из пункта 5 делим на результат из пункта 6? Не понятно…
EdgeStone: 6) используем 252-дневное нормальное распределение z-оценки или ранг процентиля метрики хаоса/стабильности;
Z оценка = (значение — среднее ) / стандартное отклонение
Z оценку величины из пункта 5) берёт по выбоки из 252 дней
Я так понимаю.
dobrachev: EdgeStone: Большое спасибо за пояснение!
EdgeStone: dobrachev: Да не за что ))
Какие у вас мысли по поводу идеи этой статьи?
Блин, вот если задуматься, и если всё на самом деле, как написано в этой статье, то тут по сути поймано не описываемое трендом и волатильностью свойство рынка, что типа локальной стационарности распределения временного ценового ряда, причём вчисляемое таким предельно простым способом,
это ж в некотором роде идеальный фильтр — есть стационарность торгуй алго, нет сиди без позы.
Надо это покапать поглубже.